set.seed(2022)第3章のRコード
第3章 確率論の基礎
乱数の設定
3.1.2 試行と事象
coin <- c("Head", "Tail")
sample(coin, 100, replace = TRUE) [1] "Tail" "Head" "Tail" "Head" "Head" "Tail" "Tail" "Head" "Tail" "Tail"
[11] "Head" "Head" "Tail" "Tail" "Head" "Head" "Tail" "Head" "Tail" "Tail"
[21] "Head" "Head" "Head" "Tail" "Head" "Tail" "Tail" "Head" "Head" "Tail"
[31] "Head" "Tail" "Tail" "Tail" "Head" "Head" "Tail" "Head" "Head" "Tail"
[41] "Head" "Tail" "Tail" "Tail" "Head" "Tail" "Head" "Tail" "Tail" "Tail"
[51] "Head" "Tail" "Head" "Head" "Tail" "Head" "Head" "Head" "Head" "Tail"
[61] "Head" "Tail" "Head" "Head" "Tail" "Tail" "Head" "Head" "Tail" "Head"
[71] "Tail" "Head" "Tail" "Tail" "Tail" "Head" "Tail" "Head" "Tail" "Tail"
[81] "Tail" "Tail" "Head" "Head" "Head" "Tail" "Head" "Tail" "Tail" "Head"
[91] "Tail" "Tail" "Tail" "Head" "Tail" "Head" "Tail" "Tail" "Head" "Head"3.1.3 コイン投げのシミュレーション
factorial(100) / (factorial(50) ^ 2) / (2 ^ 100)[1] 0.07958924coin <- c(1, 0)
z <- sample(coin, 100, replace = TRUE)
sum(z)[1] 55S <- 100000
rec <- numeric(S)
coin <- c(1, 0)
for(i in 1:S){
z <- sample(coin, 100, replace = 100)
rec[i] <- sum(z)
}hist(rec)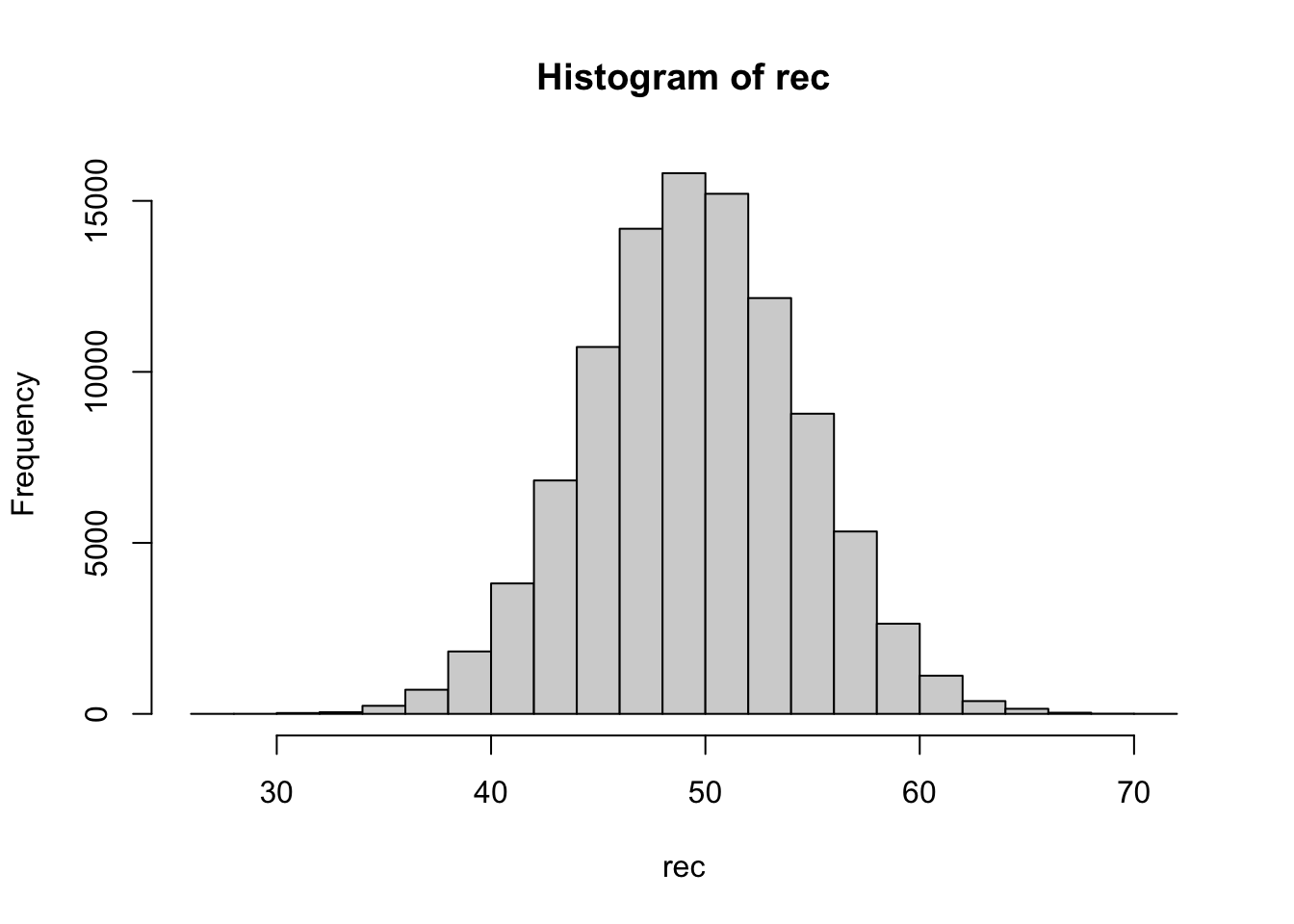
summary(rec) Min. 1st Qu. Median Mean 3rd Qu. Max.
27.00 47.00 50.00 49.99 53.00 72.00 3.1.4 論理演算によるカウントの方法
2 > 1[1] TRUE2 > 1000[1] FALSE200 == 100 * 2[1] TRUE
よくある間違い
200 = 100 * 2Error in 200 = 100 * 2 : invalid (do_set) left-hand side to assignmentTRUE + TRUE[1] 2TRUE * FALSE[1] 0count <- (rec == 50)
head(count)[1] FALSE FALSE FALSE FALSE TRUE FALSEsum(count)[1] 7966mean(count)[1] 0.079663.2.3 独立ではない例
# 独立性の確認
S <- 100000 # シミュレーション回数
X <- rnorm(S, 50, 10) # Xを抽出
Y <- rnorm(S, 50, 10) # Yを抽出
Z <- X + Y # Zを構成# Pr(X > 70) * Pr(Z > 100)
mean(X > 70) * mean(Z > 100)[1] 0.01119444# Pr(X > 70 かつ Z > 100)
mean((X > 70) * (Z > 100))[1] 0.022073.2.4 独立性と相関係数
X <- rnorm(100000, 50, 10)
Y <- rnorm(100000, 50, 10)
cor(X, Y)[1] 0.003516287Z <- - ((X - 50) ^ 2) / 10
cor(X, Z)[1] 0.01343314plot(X, Z)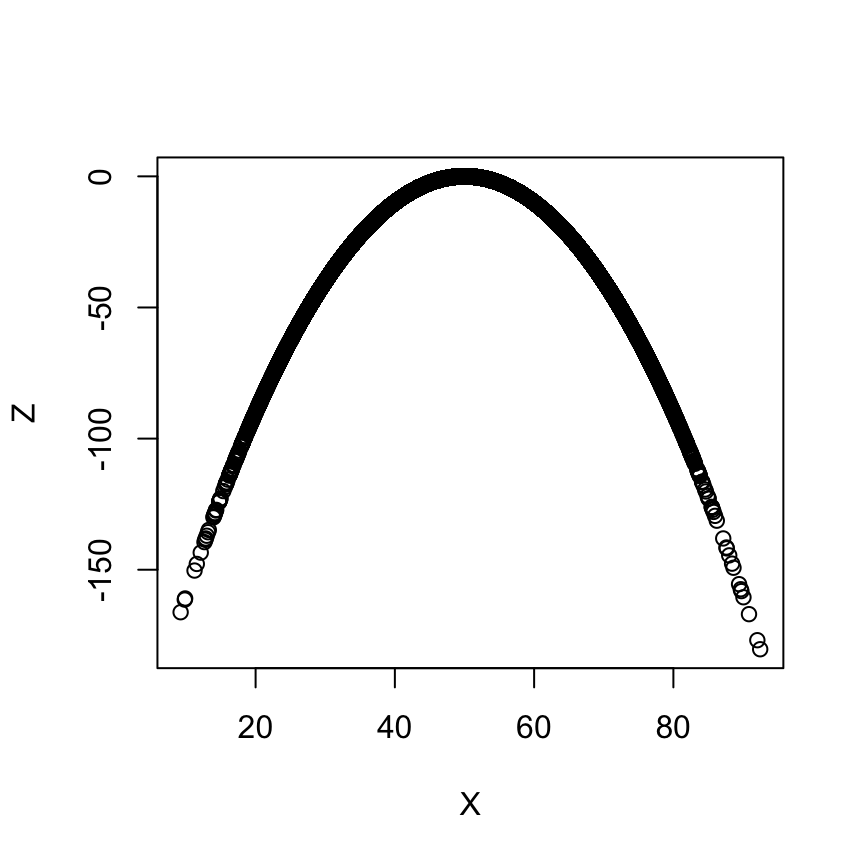
3.3.1 分布関数
curve(pnorm(x, 50, 10), 0, 100)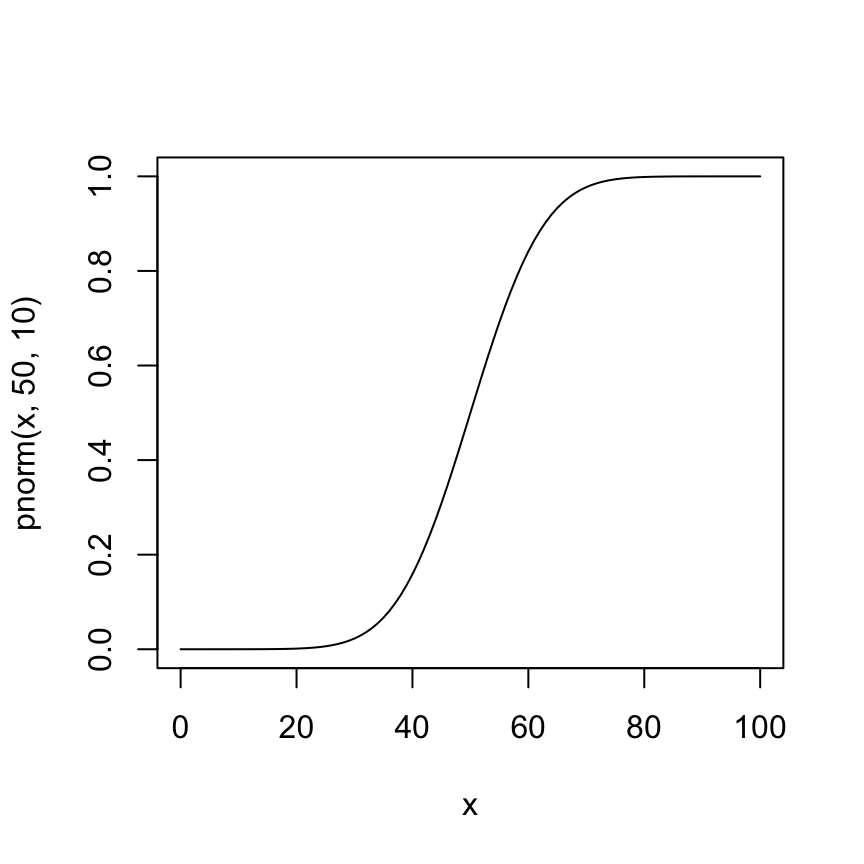
pnorm(60, 50, 10) - pnorm(40, 50, 10)[1] 0.68268953.3.2 確率密度関数
pnorm(50 + 0.1, 50, 10) - pnorm(50, 50, 10)[1] 0.003989356dnorm(50, 50, 10)[1] 0.03989423dnorm(80, 50, 10)[1] 0.0004431848curve(dnorm(x, 50, 10), 0, 100)3.3.7 データによる条件付期待値の推定
malesdata <- read.csv("wage.csv")
head(malesdata) educ exper wage
1 7 16 548
2 12 9 481
3 12 16 721
4 11 10 250
5 12 16 729
6 12 8 500summary(malesdata) educ exper wage
Min. : 1.00 Min. : 0.000 Min. : 100.0
1st Qu.:12.00 1st Qu.: 6.000 1st Qu.: 394.2
Median :13.00 Median : 8.000 Median : 537.5
Mean :13.26 Mean : 8.856 Mean : 577.3
3rd Qu.:16.00 3rd Qu.:11.000 3rd Qu.: 708.8
Max. :18.00 Max. :23.000 Max. :2404.0 plot(malesdata)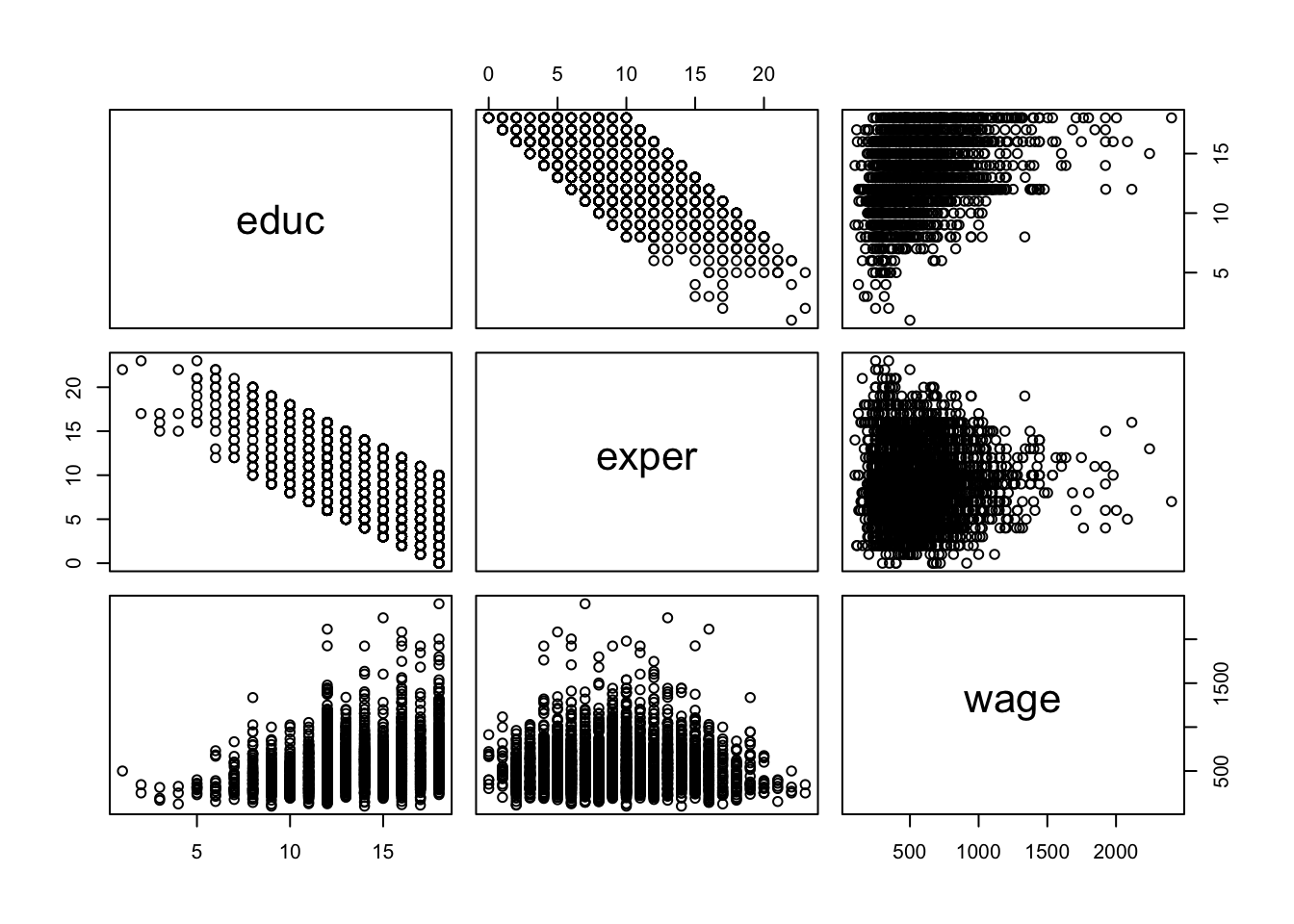
sch12 <- malesdata[malesdata$school == 12, ] # 高校卒業者の抜き出し
sch16 <- malesdata[malesdata$school == 16, ] # 学部卒業者の抜き出しexp(mean(sch12$wage)) # 高校卒業者の平均賃金[1] NaNexp(mean(sch16$wage)) # 学部卒業者の平均賃金[1] NaNsch11 <- malesdata[malesdata$school <= 11, ] # 高卒未満の抜き出し
sch12 <- malesdata[malesdata$school >= 12, ] # 高卒以上の抜き出しexp(mean(sch11$wage)) # 高卒未満の平均賃金[1] NaNexp(mean(sch12$wage)) # 高卒以上の平均賃金[1] NaN3.4.2 中心極限定理のシミュレーション
S <- 10000
n <- 10000
Zn <- numeric(S)
for(i in 1:S){
X <- rnorm(n, 50, 10)
Xbar <- mean(X)
Sn <- var(X)
Zn[i] <- sqrt(n) * (Xbar - 50) / sqrt(Sn)
}hist(Zn)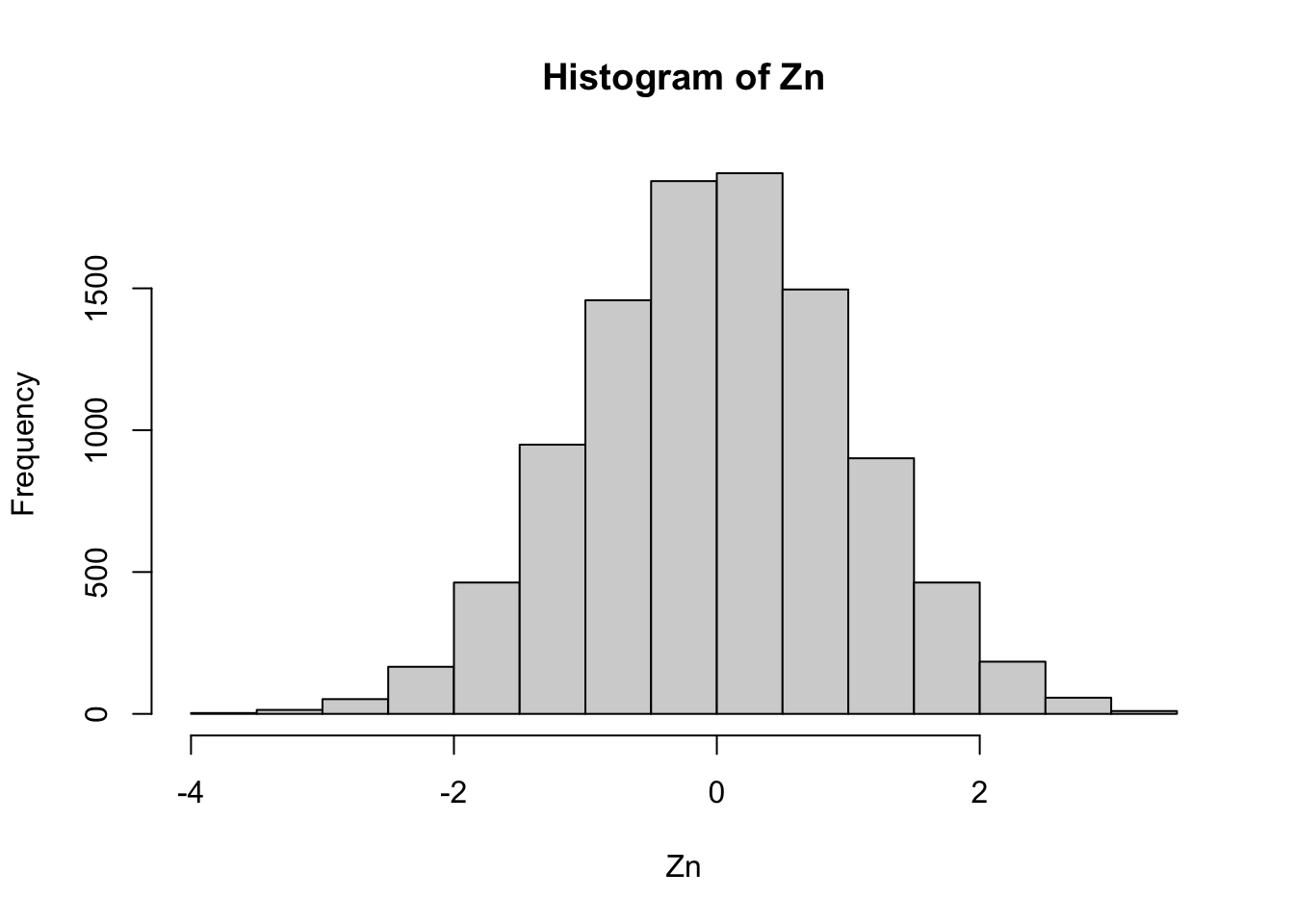
summary(Zn) Min. 1st Qu. Median Mean 3rd Qu. Max.
-3.786927 -0.685862 0.004751 0.000495 0.683271 3.361441 3.4.3 信頼区間のシミュレーション
# 信頼区間シミュレーション
S <- 10000 # シミュレーション回数
n <- 10000 # 標本の大きさ
rec <- numeric(S) # 結果記録用のベクトル
for(i in 1:S){ # 繰り返し開始
X <- rnorm(n, 50, 10) # N(50,10^2) から標本抽出
Xbar <- mean(X)
Sn <- var(X)
rec[i] <- (Xbar - 1.96 * sqrt(Sn / n) < 50) * (50 < Xbar + 1.96 * sqrt(Sn / n))
}
mean(rec) # 確率を計算[1] 0.9443.4.4 信頼区間の導出
pnorm(69.6,50,10) - pnorm(30.4,50,10)[1] 0.9500042